Ход абстрактного проекта в вакууме: модель случайным процессом
Всем добрый день. В комментариях к посту Waterfall и Agile: и всё-таки, откуда эффект? были высказаны пожелания помоделировать ход проектов. Сразу скажу, что на большее, чем на статьи в жанре «записки на салфетках» меня не хватает, увы, но тем не менее тема интересная и триальная Wolfram Mathematica доступна и умеет работать со стохастическими дифференциальными уравнениями. Например:
dprogress(t) = plan(t)*dt + risk(t)*dwt
В данном короткопосте будут подставлены конкретные plan и risk. Сразу говорю, особых чудес не будет.
plan(t) — это скорость прогресса по времени,
risk(t) — это (отрицательная) добавка к скорости, призванная отразить задержки в выполнении задач, появление новых задач и вообще всяческие проблемы. Далее риск будет равен -riskconstant * plan(t), где первый множитель, некоторая величина, больше нуля и меньше единицы.
progress(t) — собственно функция, отражающая уровень выполнения проекта (начальное значение 0, нас будет интересовать значение 1, соответствующее ста процентам).
И тут же, глядя в уравнение, можно сказать.
| Чтобы проект вообще завершился, необходимо чтобы риск потери прогресса не был всегда больше прироста прогресса! |
Исходя из уравнения очевидный вывод, но на практике… бывает не всегда об этом думают.
Самое интересное — это среднее время, когда процесс выйдет больше единицы. Чтобы посчитать подобное, придется воспользоваться теорией (вот этой).
Перейдем к делу и проведем небольшие исследования. За основу будут взяты четыре функции плана: константная скорость, с линейным ростом, квадратичная функция и квадратный корень.
В таблице приведены скриншоты (триальная Вольфрам Математика обломила с экспортом) результатов для riskconstant = 0.5 и времени для проверки завершения = 1.
| Константая функция | 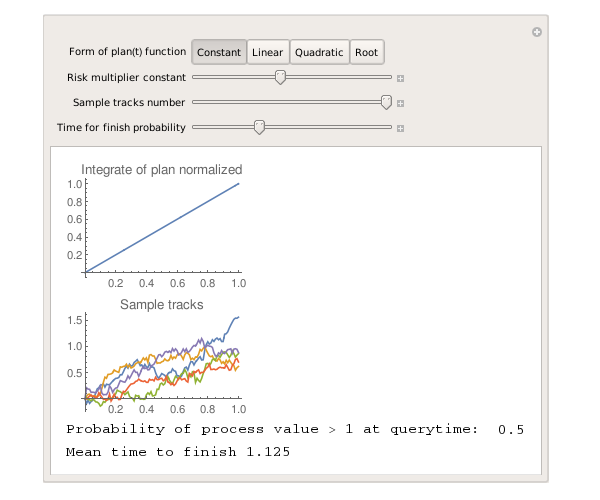 |
| Линейная функция | 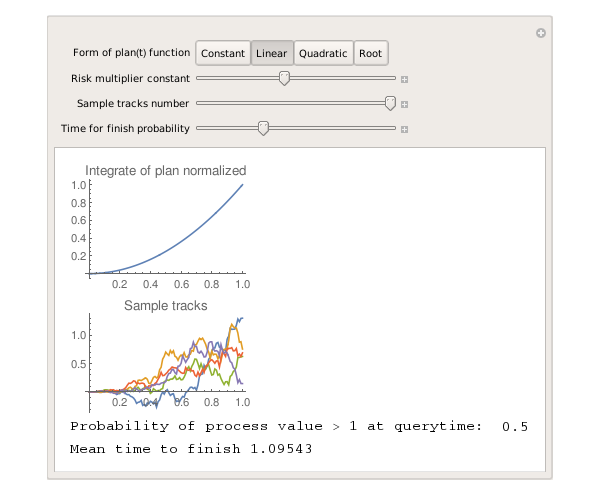 |
| Квадратичная функция | 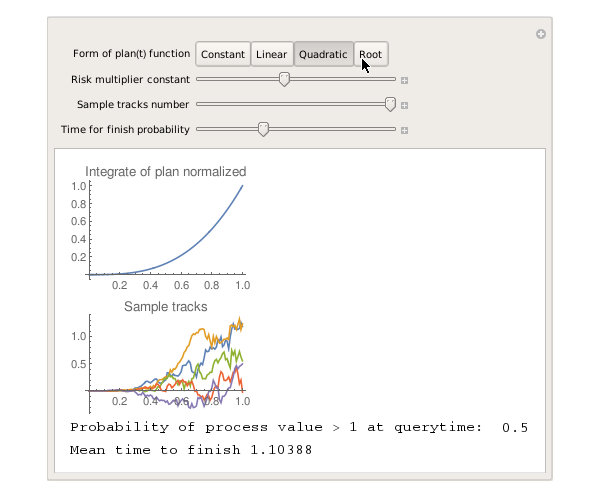 |
| Коренная функция | 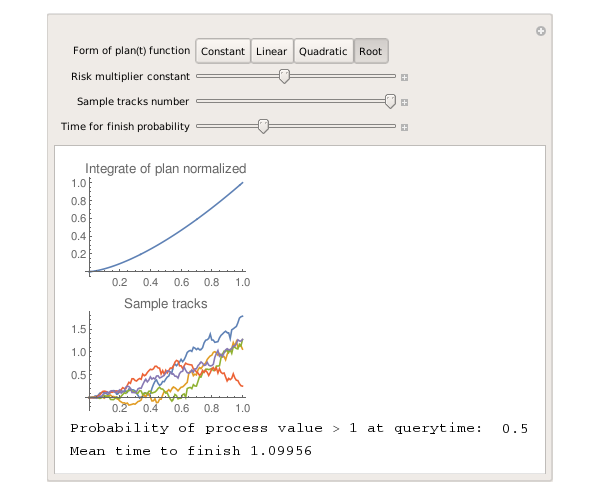 |
И какие тут можно сделать выводы? Да особо никаких не сделаешь, кроме того, что управление без обратной связи (то есть без участия progress(t) в правой части уравнения) обречено при наличии рисков иметь задержку в среднем. И да. Куда не сдвигай прирост прогресс внутри проекта (ну то есть изначально риски не перемещай вперед или назад), с вероятностью 0.5 успеешь в плановые сроки (эти 0.5 напрямую никак не связаны с riskconstant = 0.5, в данном случае это совпадение).
CDF (для версии 10.0) можно скачать здесь.
P.S. Найдете ошибки — пишите срочно, пока не закончился триал :) Через три недели карета превратится в тыкву.
P.P.S. Относительно рац. предложений — аналогично: вдруг кто посоветует уравнение с обратной связью какое конкретное, или что-то вроде.
Автор:

