Каждый раз, когда я смотрю на диаграммы Ганта [1], меня мучает один и тот же вопрос. Как? Вот как можно быть уверенным, что ресурс А, выполнит задачу Б за 5 дней? Нет, я понимаю, что есть исторические данные, есть, не побоюсь этого слова, статистика. Но вот как можно на основе всего этого делать уверенные прогнозы? Я не понимаю.
Если для вас термины «взаимозависимость событий» и «статистические отклонения» говорят что-то не только по отдельности, но и в совокупности, то статья вас вряд ли заинтересует. А вот если эти термины, употребленные в одном контексте, не говорят вам в чем проблема диаграмм Ганта, то приглашаю под кат, где на простом примере мы это и обсудим.

Для примера возьмем небольшую компанию, которая занимается разработкой веб-проектов. Работает компания уже давно, поэтому будем считать, что даже статистика по выполненным проектам за достаточно большой период у нас есть. В компании, с целью повышения эффективности, есть разделение труда. Поэтому процесс выполнения заказа состоит из четырех этапов: заключение договора с заказчиком, разработка дизайна, реализация проекта, внедрение.
Для демонстрации будут сделаны следующие предположения:

1. Каждый этап занимает от 3 до 7 дней. Например, маркетинговый отдел продает нашу услугу заказчику и заключает с ним договор. Этот процесс занимает от трех рабочих дней (клиент с типовой задачей, подписал типовой договор) до семи рабочих дней (представитель заказчика уехал в командировку, появились дополнительные согласования по договору, необходимо обсудить расширенный функционал). Дизайнеры выполняют заказ от трех (заказчик не привередлив, согласен на стандартный шаблон, надо сделать логотип, внести несколько особенностей) до семи рабочих дней (заболел дизайнер, заказчик не подписывает макет).
2. Вероятность завершить проект в каждый из дней распределена по закону непрерывного равномерного распределения [2]:
   
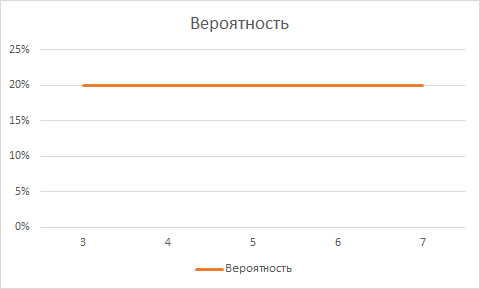
   В большинстве случаев, это будет конечно не так, скорее будет наблюдаться, что то вроде нормального распределения [3].
3. При исходных данных из пунктов 1 и 2, математическое ожидание [4] для срока заключения договора составит 3*0,2+4*0,2+5*0,2+6*0,2+7*0,2 = 5 рабочих дней. Т.е. в среднем каждый этап завершается за 5 дней.

Все эти предположения позволяют нам обсуждать сбалансированную систему. Или, иными словами, систему, в которой на каждый этап, хотя бы в среднем уходит одинаковое количество дней. Если у вас все устроено именно так, то напишите об этом в комментариях, я вам позавидую белой завистью, т.к. еще не видел организаций без «узких звеньев», а вы в такой уже работаете.
Все, с введением заканчиваю, перехожу к теме.
Давайте построим первую диаграмму Ганта. На этой диаграмме, мы, зная о том, что средний срок выполнения этапа 5 рабочих дней, получим сколько времени у нас займет реализация 5 проектов:

На данной диаграмме выражено классическое допущение, что отставание одних этапов, компенсируется опережением других, в среднем то – пять дней. Но есть один маленький нюанс. Какой? Давайте покажу на примере. Начнем с первого этапа.

Как видно, первый этап укладывается в наше предположение. Т.е. замедление одних этапов, компенсируется ускорением других. Но, если у нас присутствует упомянутая «взаимозависимость событий», то со вторым этапом ситуация наблюдается не такая радужная:

Обратили внимание, что вместо тридцатого рабочего дня, второй этап пятого проекта закончился на тридцать третий рабочий день? А тут еще и страшный сон «менеджера» вырисовывается: 13, 14, 18, 19, и 20 рабочий день сотрудникам нечего делать. Ну и последняя картинка:

Именно сейчас у читателя должна появиться мысль: «Да он просто пример такой подстроил!». К сожалению, не подстроил. Проведя моделирование 1000 раз, даже в таких тепличных условиях, с математическим ожиданием на всех этапах в 5 рабочих дней, вероятность завершения проекта в зависимости от дня выглядит так:

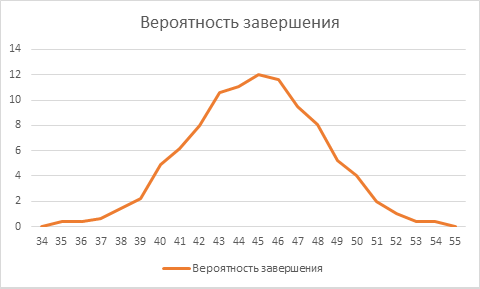
Да, наиболее вероятное значение 44-45 дней, но давайте построим еще и график, какова вероятность завершить проекты к заданному дню:

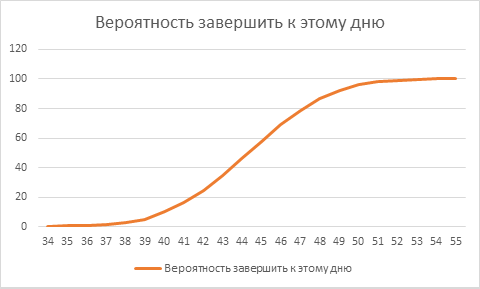
К сороковому дню, вероятность завершить проекты примерно равна 10%. К 44-45 дню вероятность завершить все проекты составляет всего 50%. Т.е., если мы согласны обманывать заказчика по срокам не чаще, чем один раз из пяти, то надо брать 80%, а это уже 48 день. Получается отклонение от первоначального плана в 40 дней на 20%. И это в условиях сбалансированной системы, с предположением, что все проекты одинаковы.
Ситуация чуть улучшается, когда у нас вероятность завершения распределена по нормальному закону. Например, при математическом ожидании равном 5 и дисперсии [5] равной 0,5. В этом случае вероятность завершить этап в один из дней от 3 до 7 будет распределена следующим образом:

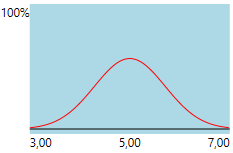
С таким распределением вероятность завершения к определенному дню будет иметь вид:

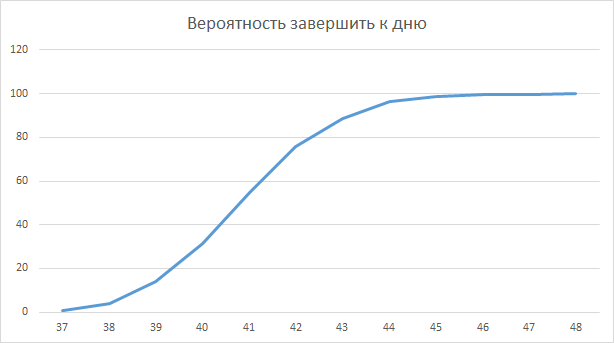
Ситуация улучшилась. В запланированные 40 дней, мы будем успевать уже с вероятностью 30%. А к 43 рабочему дню вероятность составит 80%. К сожалению, в реальных проектах такая дисперсия может быть только при очень высокой повторяемости. Например, на сборочном конвейере. При разработке программного обеспечения дисперсия будет значительно выше, т.к. проекты в большинстве своем уникальные и разброс трудозатрат на них может быть весьма велик.
Ну и завершая, маленькая зарисовка для привлечения внимания к следующей статье. Как вы считаете, что произойдет с «идеальной» диаграммой Ганта, если на первом, третьем и четвертом этапе сдвинуть математическое ожидание на 4, в на втором этапе на 7. Т.е. три этапа будут быстрее в среднем на один день, а один этап длиннее на два?

Диаграмма Ганта и вероятность завершить к дню

Впечатляет? Т.е., теоретически сократив разработку проекта на 1 день, мы замедлили разработку 5 проектов на 6 дней. Но, зато, если мы посмотрим на диаграмму вероятности завершения 5 проектов к заданному дню, то там:

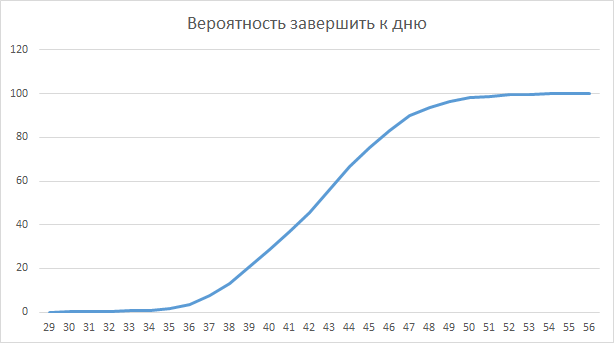
С вероятностью 80% мы завершим к 46 дню, который получен с диаграммы Ганта. Привлек внимание? Ну и хорошо, встретимся в следующей статье.

P.s. За вычитывание и советы по статье большая благодарность Андрею Потапову и CrazyViper. С днем программиста вас и всех читателей Хабра!

1. http://ru.wikipedia.org/wiki/Диаграмма Ганта [к тексту]
2. http://ru.wikipedia.org/wiki/Непрерывное равномерное распределение [к тексту]
3. http://ru.wikipedia.org/wiki/Нормальное распределение [к тексту]
4. http://ru.wikipedia.org/wiki/Математическое ожидание [к тексту]
5. http://ru.wikipedia.org/wiki/Дисперсия случайной величины [к тексту]

Автор: Teacher

Источник