Нелинейные зависимости в регрессии. Как линейная регрессия может описать параболу, синусоиду и твою зарплату (хихи)
Разбираем стажерско-джуновский вопрос с собеседования.
Вопрос с собеса:
«Можем ли мы описать параболу линейной регрессией?»
Сначала поговорим о задачи регресии в целом.
Элементарная задача регрессии
Давайте представим 6 типичных выпускников школы. Нас интересует один вопрос: как количество пройденных университетских курсов влияет на их текущий доход?
Знакомьтесь, наши «тюбики»:
-
Аркадий
-
Бросил учёбу после 1 курса
-
Работает в Маке
-
-
Анатолий (лучший друг Аркадия)
-
Держался до 2 курса, потом тоже пошёл работать в Мак
-
-
Матвей
-
Ушёл с 3 курса
-
Стажёр-аналитик в Ы-банке
-
-
Мефодий
-
Окончил бакалавриат
-
Аналитик в том же Ы-банке
-
-
Леонид
-
Окончил бакалавриат
-
Посмотрел на Матвея и Мефодия → пошёл в банк
-
-
Авакум
-
Пошёл в магистратуру
-
Через 2 года после выпуска мы собрали их доходы в одну таблицу:
|
Имя |
Годы обучения |
Зарплата (в тыс. руб.) |
|
Аркадий |
1 год |
30 тыс. руб. |
|
Анатолий |
2 года |
30 тыс. руб. |
|
Матвей |
3 года |
60 тыс. руб. |
|
Мефодий |
Окончил бакалавриат |
80 тыс. руб. |
|
Леонид |
Окончил бакалавриат |
70 тыс. руб. |
|
Авакум |
Пошел в магистратуру |
? |
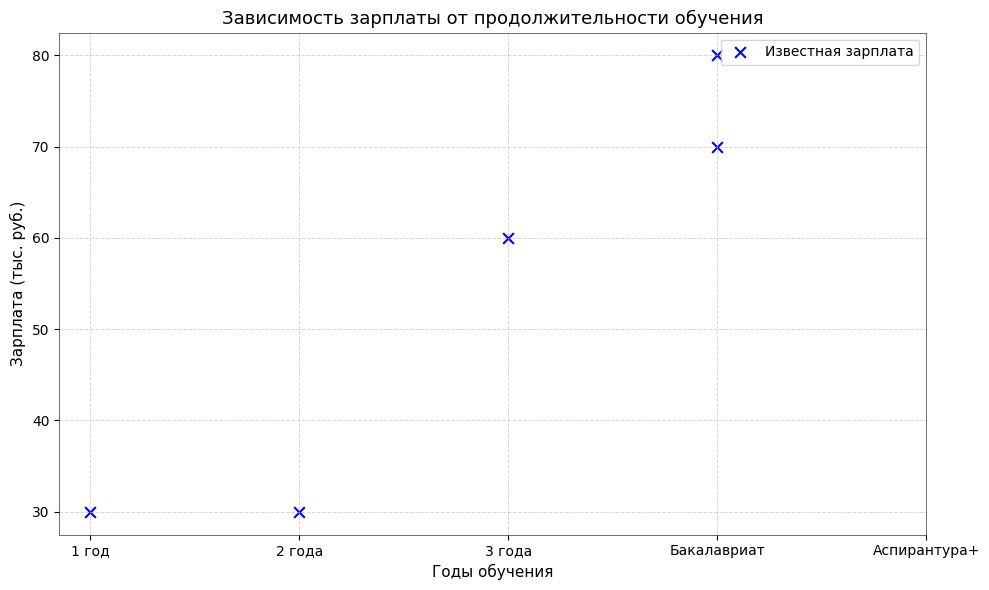
Что бросается в глаза?
Очевидно, что зависимость между годами учёбы и зарплатой будто бы все же есть.
Обучим все же регрессию на наших данных:
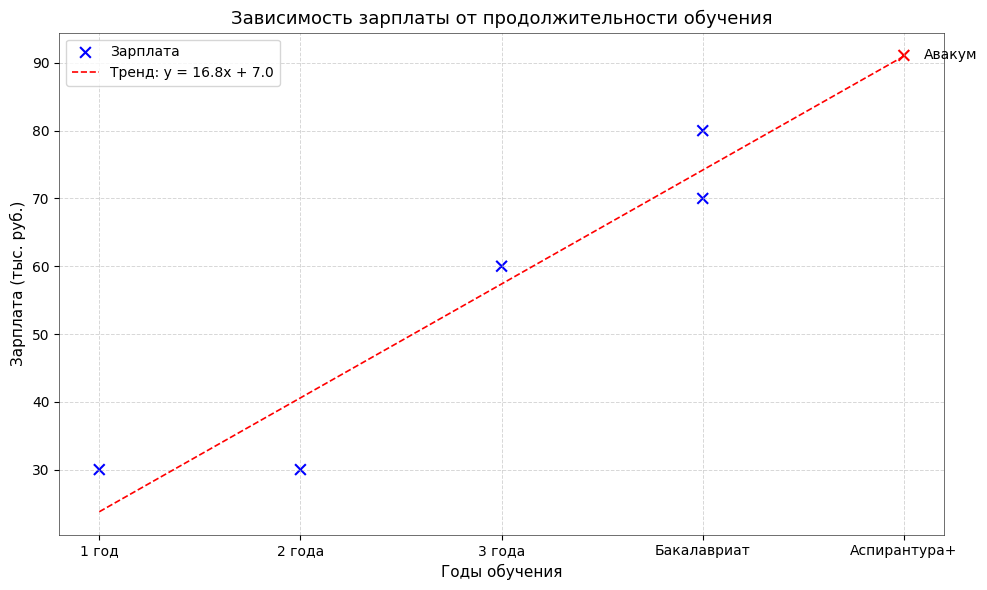
Используя данные о зарплатах и образовании, мы можем построить регрессионную модель и сделать прогнозы и понять сколько бы примерно зарабатывал бы Авакум, если бы пошел работать прямо сейчас.
Математическая формулировка линейной регрессии
Линейная регрессия описывается уравнением:
где:
-
Y – предсказанная зарплата,
-
X – количество оконченных курсов в универе,
-
a – начальное значение (например, доход без образования/ сразу после выпуска),
-
b – влияние образования на зарплату.
Расширение регрессии до множественной:
Любая модель — это лишь приближение реальности. Часто более сложные модели описывают действительность чуть точнее, чем упрощённые.
Поэтому добавим в нашу модель информацию об опыте работы. Предположим, что некоторые начали работать ещё в школе или успели получить определённый опыт.
Соберем данные об их опыте работы и сделает 3D график:
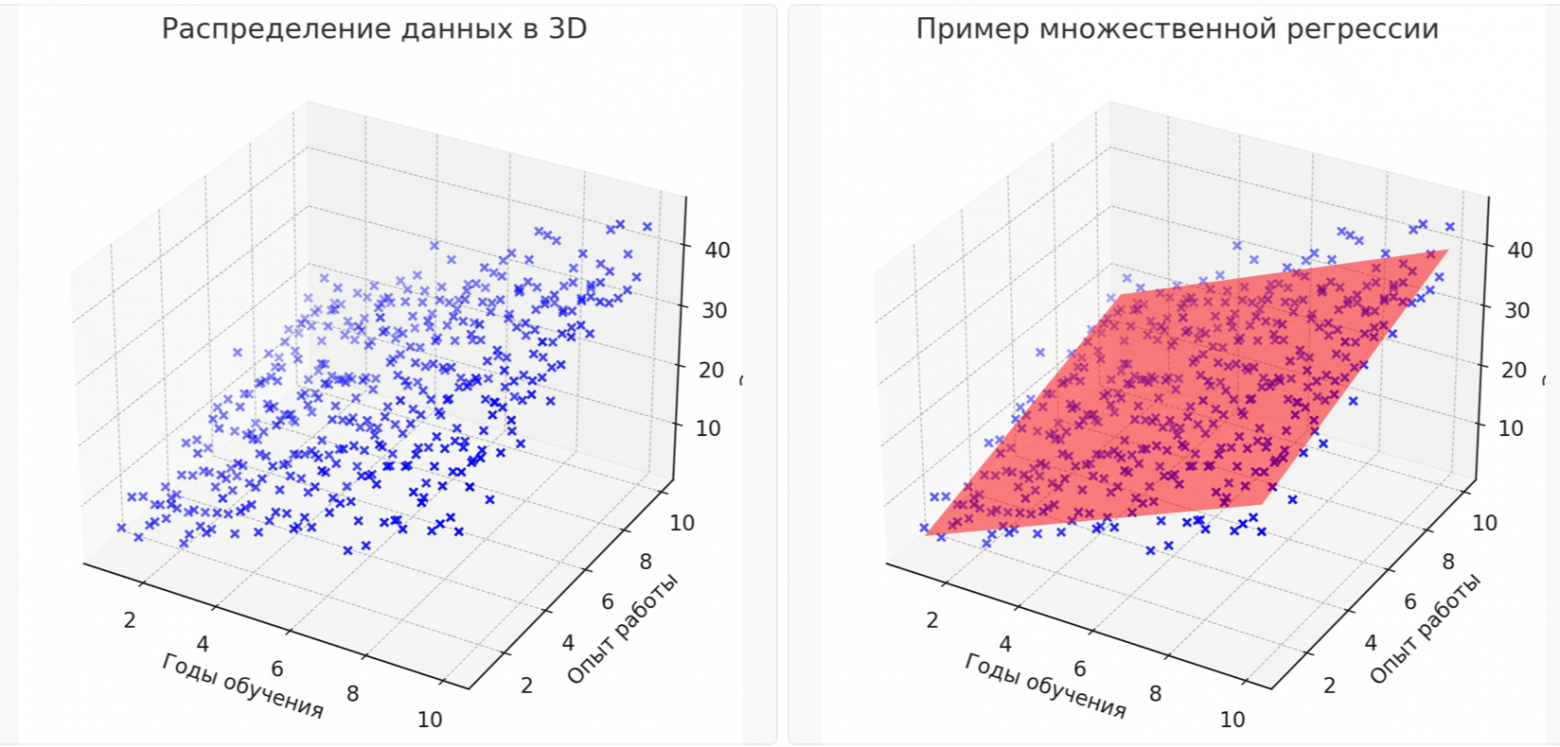
Тогда можем увидеть, что, допустим, Аркадий, несмотря на то что закончил только один курс университета, получает больше, потому что до этого в школе уже какое-то время проработал где-то, а Анатолий — нет.
А теперь магия. Добавляем нелинейность!
Расширим нашу опрашиваемую выборку и посмотрим внимательно на данные:
|
Имя |
Годы обучения |
Зарплата (тыс. руб.) |
|
Аркадий |
1 год |
25 |
|
Анатолий |
2 года |
35 |
|
Матвей |
3 года |
75 |
|
Мефодий |
4 года (бакалавриат) |
110 |
|
Леонид |
4 года (бакалавриат) |
105 |
|
Геннадий |
5 лет (аспирантура) |
145 |
|
Авакум |
6 лет (аспирантура) |
170 |
|
Альберт |
7 лет (аспирантура) |
190 |
|
Иннокентий |
8 лет (аспирантура) |
205 |
|
Всеволод |
9 лет (аспирантура) |
215 |
|
Платон |
10 лет (аспирантура) |
220 |
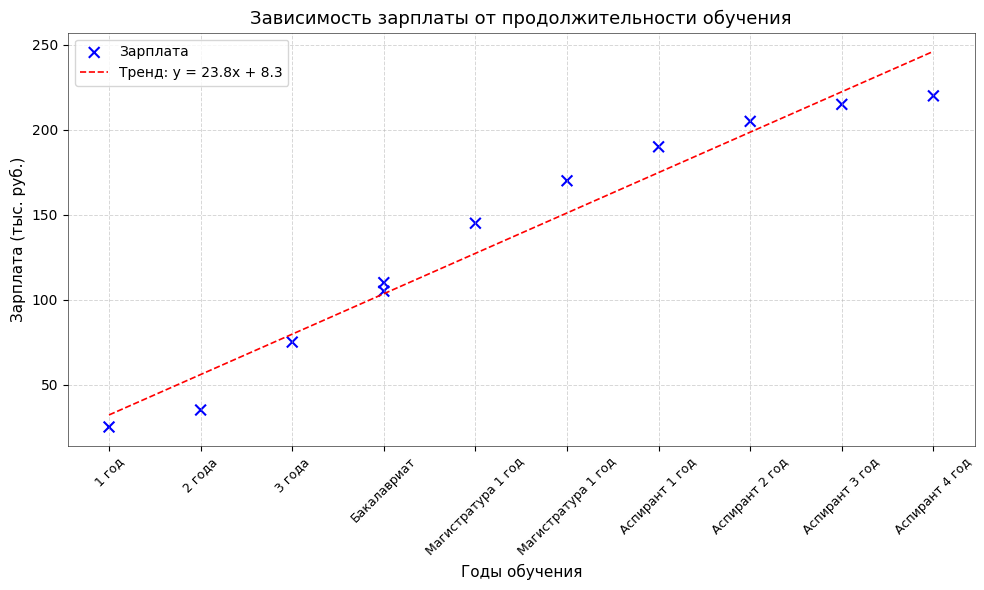
Видим, что с какого-то момента зарплата растет уже как-то не так бодро, как на начальных стадиях (а хотелось бы).
И регрессия наша уже тоже как-то не очень то попадает.
И что теперь? Все сломалось? — Ноуп.
Попробуем вместо переменной взять логарифм от нашей переменной (ln(годы обучения)).
Важно: линейная регрессия называется линейной не из-за прямой на графике, а потому что линейна по параметрам. Мы можем преобразовывать признаки (X), главное — сохранять линейность коэффициентов (a, b, c…).
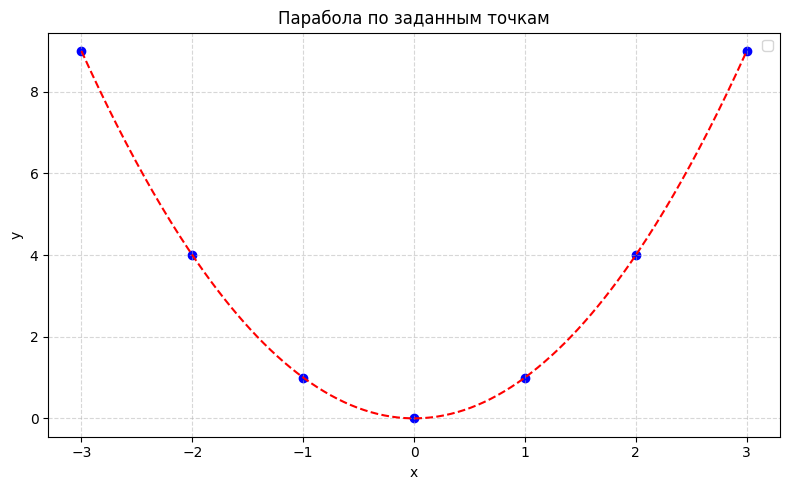
Так уравнениеформально остается линейной регрессией, хоть и описывает параболу.
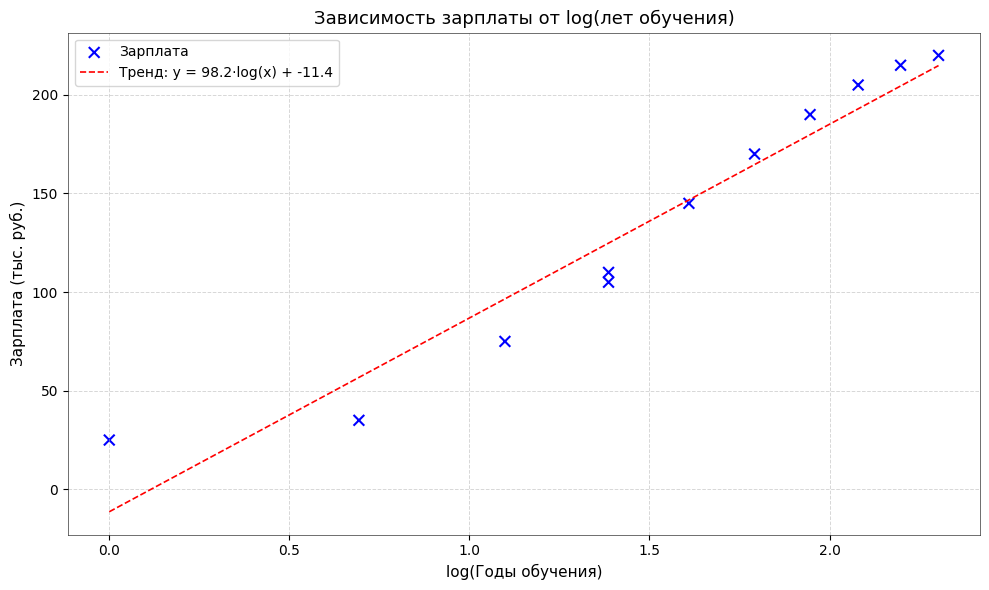
И вуаля. Наши точки уже гораздо лучше ложатся на прямую.
Этот процесс называется «линеаризацией переменных».
Ответим же теперь на вопрос собеса. Можем ли мы описать линейной регрессией параболу?
Ес, оф хорс. Мы хотим получить формулу вида , а что будет внутри этого Х нам абсолютно фиолетово (там может быть хоть полином 120 степени). Поэтому запихнем внутрь
нашу переменную
. Чтобы нам это сделать нам нужно применить преобразование к х и смотреть теперь на
как на обычную колонку.
|
|
|
|
|---|---|---|
|
9 |
-3 |
9 |
|
4 |
-2 |
4 |
|
1 |
-1 |
1 |
|
0 |
0 |
0 |
|
1 |
1 |
1 |
|
4 |
2 |
4 |
|
9 |
3 |
9 |
Теперь наша парабола прекрасно описывается уравнением , а оно линейное!
Хочешь ещё? Смотри подробнее в статье Яндекса по линейным моделям:
Автор: GOOGLovskaya

